Author:
R.Gowri Shankar1 , D.R. Ananthi, 2Published in
Journal of Science Technology and Research( Volume , Issue )
[1] A. D. Booth, “A signed binary multiplication technique,” Quart. J. Mech. Appl. Math., vol. 4,
no. 2, pp. 236–240, 1951.
[2] C. S. Wallace, “A suggestion for a fast multiplier,” IEEE Trans. Electron. Comput., vol. EC-13,
no. 1, pp. 14–17, Feb. 1964.
[3] L. Dadda, “Some schemes for parallel multipliers,” Alta Frequenza, vol. 34, no. 5, pp. 349–356,
Mar. 1965.
[4] E. L. Braun, Digital Computer Design: Logic, Circuitry, and Synthesis. New York, NY, USA:
Academic, 2014.
[5] C. R. Baugh and B. A. Wooley, “A two’s complement parallel array multiplication algorithm,”
IEEE Trans. Comput., vol. C-100, no. 12, pp. 1045–1047, Dec. 1973.
[6] D. Hampel, K. E. McGuire, and K. J. Prost, “CMOS/SOS serial parallel multiplier,” IEEE J. SolidState Circuits, vol. SSC-10, no. 5, pp. 307–313, Oct. 1975.
[7] Z. Huang and M. D. Ercegovac, “High-performance low-power leftto-right array multiplier
design,” IEEE Trans. Comput., vol. 54, no. 3, pp. 272–283, Mar. 2005.
[8] J. Prummel et al., “A 10 mW Bluetooth low-energy transceiver with on-chip matching,” IEEE
J. Solid-State Circuits, vol. 50, no. 12, pp. 3077–3088, Dec. 2015.
[9] J. Fadavi-Ardekani, “M×N Booth encoded multiplier generator using optimized Wallace trees,”
IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 1, no. 2, pp. 120–125, Jun. 1993.
[10] N. Itoh, Y. Naemura, H. Makino, Y. Nakase, T. Yoshihara, and Y. Horiba, “A 600-MHz 54×54-
bit multiplier with rectangular-styled Wallace tree,” IEEE J. Solid-State Circuits, vol. 36, no. 2, pp.
249–257, Feb. 2001.
[11] V. G. Oklobdzija, D. Villeger, and S. S. Liu, “A method for speed optimized partial product
reduction and generation of fast parallel multipliers using an algorithmic approach,” IEEE Trans.
Comput., vol. 45, no. 3, pp. 294–306, Mar. 1996.
[12] P. F. Stelling, C. U. Martel, V. G. Oklobdzija, and R. Ravi, “Optimal circuits for parallel
multipliers,” IEEE Trans. Comput., vol. 47, no. 3, pp. 273–285, Mar. 1998.
[13] A. A. Farooqui and V. G. Oklobdzija, “General data-path organization of a MAC unit for VLSI
implementation of DSP processors,” in Proc. IEEE Int. Symp. Circuits Syst. (ISCAS), vol. 2, May/Jun.
1998, pp. 260–263.
[14] N. Petra, D. De Caro, V. Garofalo, E. Napoli, and A. G. M. Strollo, “Truncated binary multipliers
with variable correction and minimum mean square error,” IEEE Trans. Circuits Syst. I, Reg.
Papers, vol. 57, no. 6, pp. 1312–1325, Jun. 2010.
[15] J.-Y. Kang and J.-L. Gaudiot, “A simple high-speed multiplier design,” IEEE Trans. Comput.,
vol. 55, no. 10, pp. 1253–1258, Oct. 2006.
[16] S.-R. Kuang, J.-P. Wang, and C.-Y. Guo, “Modified booth multipliers with a regular partial
product array,” IEEE Trans. Circuits Syst. II, Exp. Briefs, vol. 56, no. 5, pp. 404–408, May 2009.
[17] W. Yan, M. D. Ercegovac, and H. Chen, “An energy-efficient multiplier with fully overlapped
partial products reduction and final addition,” IEEE Trans. Circuits Syst. I, Reg. Papers, vol. 63, no.
11, pp. 1954–1963, Nov. 2016.
[18] J. Mori et al., “A 10 ns 54×54 b parallel structured full array multiplier with 0.5 μm CMOS
technology,” IEEE J. Solid-State Circuits, vol. 26, no. 4, pp. 600–606, Apr. 1991.
[19] N. Ohkubo et al., “A 4.4 ns CMOS 54×54-b multiplier using passtransistor multiplexer,” IEEE
J. Solid-State Circuits, vol. 30, no. 3, pp. 251–257, Mar. 1995.
[20] C.-H. Chang, J. Gu, and M. Zhang, “Ultra low-voltage low-power CMOS 4-2 and 5-2
compressors for fast arithmetic circuits,” IEEE Trans. Circuits Syst. I, Reg. Papers, vol. 51, no. 10,
pp. 1985–1997, Oct. 2004.
[21] L.-D. Van and J.-H. Tu, “Power-efficient pipelined reconfigurable fixed width Baugh-Wooley
multipliers,” IEEE Trans. Comput., vol. 58, no. 10, pp. 1346–1355, Oct. 2009.5.
[22] Rajagopal, R., Karthick, R., Meenalochini, P., & Kalaichelvi, T. (2023). Deep Convolutional
Spiking Neural Network optimized with Arithmetic optimization algorithm for lung disease
detection using chest X-ray images. Biomedical Signal Processing and Control, 79, 104197.
[23] Srinivas, T. Aditya Sai, B. Ravindra Babu, Miskir Solomon Tsige, R. Rajagopal, S. Devi, and
Subrata Chowdhury. “Effective implementation of the Prototype of a digital stethoscope using a
Smartphone.” In 2022 International Conference on Innovative Computing, Intelligent
Communication and Smart Electrical Systems (ICSES), pp. 1-8. IEEE, 2022.
[24] Rajagopal, R., M. Karthik, M. Soni, Narayan Krishan Vyas, S. Hemavathi, and M. R. Arun.
“Monitoring the high-speed engine application using ferro magnetic system.” Materials Today:
Proceedings (2022).
[25] Babu, P. Ramesh, Vemuri Kusuma Priya, N. Drawin, R. Thiagarajan, and R. Krishnamoorthy.
“Enhanced Hybrid Resource Scheduler for an Institution Employing NB-RR Scheduling.” In 2022
8th International Conference on Smart Structures and Systems (ICSSS), pp. 1-6. IEEE, 2022.
[26] Jose, S. Edwin, R. Lal Raja Singh, and R. Rajagopal. “Automatic and real time classification of
power quality disturbance using statistical moments.” AIP Conference Proceedings. Vol. 2327.
No. 1. AIP Publishing LLC, 2021.
[27] Rajagopal, R., and S. Edwin Jose. “An Efficient Framework for Locating Stroke in Brain MRI
Images Using Radon Transform and Convolutional Neural Networks.” In Next Generation of
Internet of Things, pp. 385-395. Springer, Singapore, 2021.
[28] Rajagopal, R., and P. Subbaiah. “A survey on liver tumor detection and segmentation
methods.” ARPN Journal of Engineering and Applied Sciences 10, no. 6 (2015): 2681-2685
[29 Rajagopal, R., & Subbiah, P. (2014). Computer aided detection of liver tumor using SVM
classifier. International Journal of Advanced Research in Electrical, Electronics and
Instrumentation Engineering, 3(6), 10170-7.
[30] Rajagopal, R. (2019). Glioma brain tumor detection and segmentation using weighting
random forest classifier with optimized ant colony features. International Journal of imaging
systems and technology, 29(3), 353-359.
ABSTRACT:
Approximate computing significantly enhances digital circuit performance by reducing hardware complexity, especially in error-resilient applications like DSP, multimedia, and machine learning. To improve these applications, particularly Convolutional Neural Networks, we designed a truncation-based Booth multiplier using multi-level compressors such as 4:2, 5:2, and 6:3 counters. We created a compensation circuit through selective Karnaugh map modifications to handle carries from truncated parts. By mapping efficiently, we reduced hardware and output errors simultaneously. We introduced Truncated and Approximate Booth Multipliers using Compressors and Counters (TABM-CC), offering multiple designs based on truncation factor www, balancing power and accuracy. Our proposed TABM-CC architecture outperforms existing multipliers in both accuracy and Area-Power efficiency. Parallel multipliers, vital in DSPs, CPUs, and multimedia systems, benefit significantly from this approach. Since most CPUs contain multipliers in critical signal paths, our design reduces delay and complexity, optimizing real-time digital processing in high-performance and low-power systems.
INTRODUCTION:
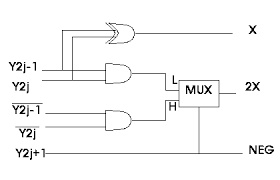
Parallel multipliers serve as key components in digital hardware, including SoCs and GPUs. They directly influence system performance, prompting researchers to continuously improve their speed, power efficiency, and size. In typical binary multiplication, designers follow a four-step process: digit recoding, digit-wise multiplication, reduction of partial products, and final carry-propagate addition. Full adder (FA)-based architectures, while common, suffer from cascading delays and high gate counts. To address this, we employed compressor networks—particularly 5:2 and 7:2 designs—to reduce latency and power consumption. We optimized these compressors by enhancing horizontal carry paths and introducing neutral output states, which significantly reduced vertical signal load. For instance, our 5:2 compressor achieved a 303-ps delay with fewer than three XOR gate delays. This optimization led to a 7:2 compressor with a four-XOR latency. These speed gains, paired with low power and compact area, make our designs ideal for energy-efficient real-time multipliers in modern digital applications.